在机器学习算法中,决策树算法是一种经常使用的预测算法。今天我们通过介绍决策树算法的实现和决策树算法的优缺点,来了解一下决策树算法。
1.算法概述
决策树算法是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法。
分类算法是利用训练样本集获得分类函数即分类模型(分类器),从而实现将数据集中的样本划分到各个类中。分类模型通过学习训练样本中属性集与类别之间的潜在关系,并以此为依据对新样本属于哪一类进行预测。
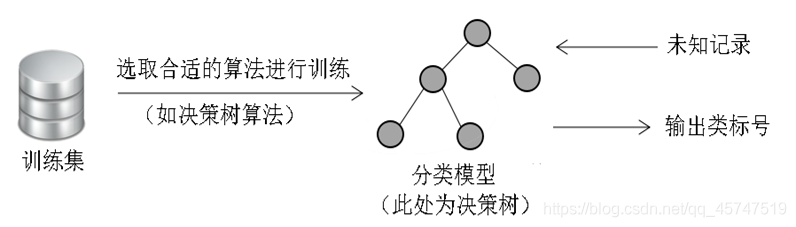
决策树算法是直观运用概率分析的一种图解法,是一种十分常用的分类方法,属于有监督学习。
决策树是一种树形结构,其中每个内部结点表示在一个属性上的测试,每个分支代表一个测试输出,每个叶子结点代表一种类别。
决策树学习是以实例为基础的归纳学习,它采用自顶向下的递归方法,其基本思想是以信息熵为度量构造一颗熵值下降最快的树,到叶子结点处的熵值为零,此时每个叶子节点中的实例都属于同一类。
决策树学习算法的最大优点是,它可以自学习,在学习的过程中不需要使用者了解过多的背景知识,只需要对训练实例进行较好的标注,就能够进行学习。
2.算法种类
ID3算法
- ID3算法中根据信息论的信息增益评估和选择特征。每次选择信息增益最大的候选特征,作为判断模块。
- 信息增益与属性的值域大小成正比。属性取值种类越多,越有可能成为分裂属性。
- ID3也不能处理连续分布的数据。
C4.5算法
- C4.5算法使用信息增益率代替信息增益,进行特征选择,克服了信息增益选择特征时偏向于特征值个数较多的不足。
- C4.5算法具体算法步骤与ID3类似。
- C4.5能够完成对连续属性的离散化处理,能够对不完整数据进行处理。
C5.0算法
- C5.0算法是Quinlan在C4.5算法的基础上提出的商用改进版本,目的是对含有大量数据的数据集进行分析。
- C5.0算法与C4.5算法相比有以下优势:
- 决策树构建时间要比C4.5算法快上数倍,同时生成的决策树规模也更小,拥有更少的叶子结点数
- 使用了提升法(boosting),组合多个决策树来做出分类,使准确率大大提高
- 提供可选项由使用者视情况决定,例如是否考虑样本的权重、样本错误分类成本等
CART算法
- CART决策树的生成就是递归地构建二叉决策树的过程。
- CART用基尼系数最小化准则来进行特征选择,生成二叉树。
- Gini系数计算公式:
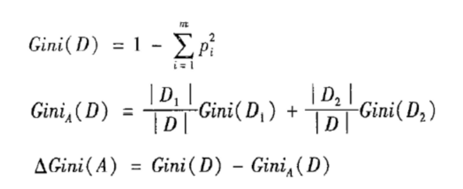
3.算法示例

在机器学习中,决策树是一种预测模型,它代表的是对象属性与对象值之间的一种映射关系。
决策树的目的是拟合一个可以通过指定输入值预测最终输出值得模型。

4.决策树构建示例
描述

分析
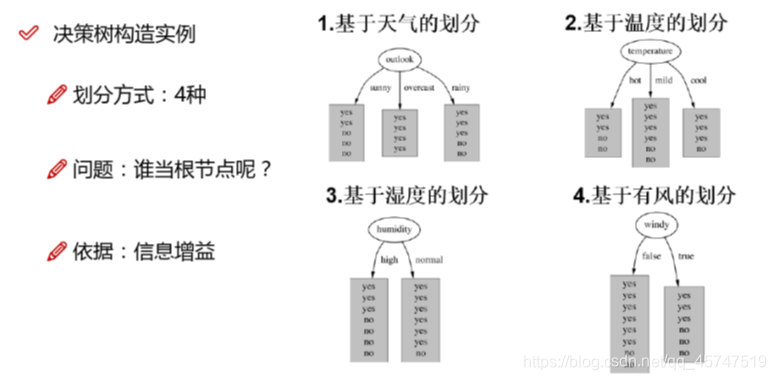
计算

结论

5.算法实现步骤
选择属性是构建一颗决策树非常关键的一步,被选择的属性会成为决策树的一个节点,并且不断递归地选择最优的属性就可以最终构建决策树。
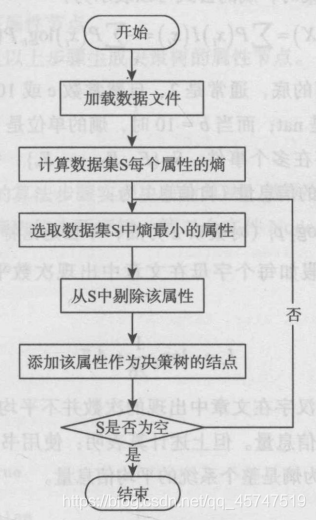
计算数据集S中的每个属性的熵 H(xi)选取数据集S中熵值最小(或者信息增益最大,两者等价)的属性在决策树上生成该属性节点使用剩余结点重复以上步骤生成决策树的属性节点
6.算法相关概念
熵
1948年,香农提出了“信息熵”的概念,熵是接收的每条信息中所包含信息的平均量,是不确定性的量度,而不是确定性的量度,因为越随机的信源的熵越大。熵被定义为概率分布的对数的相反数。
信息熵的公式:
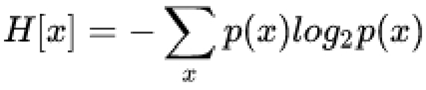
信息增益
“信息增益”是用来衡量一个属性区分数据样本的能力,当使用某一个属性作为一棵决策树的根节点时,该属性的信息增益量就越大。决策树会选择最大化信息增益来对结点进行划分。
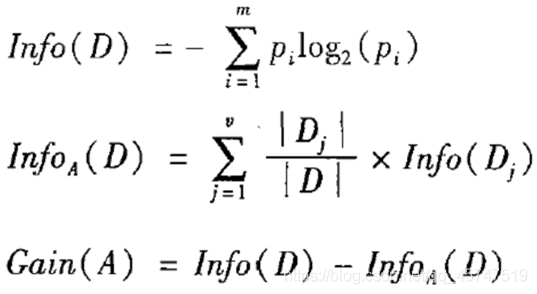
7.算法实现代码
import numpy as np
import math
from collections import Counter
# 创建数据
def create_data():
X1 = np.random.rand(50, 1)*100
X2 = np.random.rand(50, 1)*100
X3 = np.random.rand(50, 1)*100
def f(x):
return 2 if x > 70 else 1 if x > 40 else 0
y = X1 + X2 + X3
Y = y > 150
Y = Y + 0
r = map(f, X1)
X1 = list(r)
r = map(f, X2)
X2 = list(r)
r = map(f, X3)
X3 = list(r)
x = np.c_[X1, X2, X3, Y]
return x, ['courseA', 'courseB', 'courseC']
# 计算集合信息熵的函数
def calculate_info_entropy(dataset):
n = len(dataset)
# 我们用Counter统计一下Y的数量
labels = Counter(dataset[:, -1])
entropy = 0.0
# 套用信息熵公式
for k, v in labels.items():
prob = v / n
entropy -= prob * math.log(prob, 2)
return entropy
# 实现拆分函数
def split_dataset(dataset, idx):
# idx是要拆分的特征下标
splitData = defaultdict(list)
for data in dataset:
# 这里删除了idx这个特征的取值,因为用不到了
splitData[data[idx]].append(np.delete(data, idx))
return list(splitData.values()), list(splitData.keys())
# 实现特征的选择函数
def choose_feature_to_split(dataset):
n = len(dataset[0])-1
m = len(dataset)
# 切分之前的信息熵
entropy = calculate_info_entropy(dataset)
bestGain = 0.0
feature = -1
for i in range(n):
# 根据特征i切分
split_data, _ = split_dataset(dataset, i)
new_entropy = 0.0
# 计算切分后的信息熵
for data in split_data:
prob = len(data) / m
new_entropy += prob * calculate_info_entropy(data)
# 获取信息增益
gain = entropy - new_entropy
if gain > bestGain:
bestGain = gain
feature = i
return feature
# 决策树创建函数
def create_decision_tree(dataset, feature_names):
dataset = np.array(dataset)
counter = Counter(dataset[:, -1])
# 如果数据集值剩下了一类,直接返回
if len(counter) == 1:
return dataset[0, -1]
# 如果所有特征都已经切分完了,也直接返回
if len(dataset[0]) == 1:
return counter.most_common(1)[0][0]
# 寻找最佳切分的特征
fidx = choose_feature_to_split(dataset)
fname = feature_names[fidx]
node = {fname: {}}
feature_names.remove(fname)
# 递归调用,对每一个切分出来的取值递归建树
split_data, vals = split_dataset(dataset, fidx)
for data, val in zip(split_data, vals):
node[fname][val] = create_decision_tree(data, feature_names[:])
return node
# 决策树节点预测函数
def classify(node, feature_names, data):
# 获取当前节点判断的特征
key = list(node.keys())[0]
node = node[key]
idx = feature_names.index(key)
# 根据特征进行递归
pred = None
for key in node:
# 找到了对应的分叉
if data[idx] == key:
# 如果再往下依然还有子树,那么则递归,否则返回结果
if isinstance(node[key], dict):
pred = classify(node[key], feature_names, data)
else:
pred = node[key]
# 如果没有对应的分叉,则找到一个分叉返回
if pred is None:
for key in node:
if not isinstance(node[key], dict):
pred = node[key]
break
return pred
8.算法优缺点
优点:小规模数据集有效
缺点
- 处理连续变量不好
- 类别比较多时,错误增加得比较快
- 不能处理大量数据
9.算法优化
决策树算法是一种非常经典的算法,其训练过程中主要依靠获得数据间的熵及信息增益作为划分依据,分类效果较好。但一般情况下我们训练决策树均是在数据量较小的数据集进行,当训练分类器所用的训练数据足够大时,决策树会出现树身过高、拟合效果差等问题。因此,如何高效准确的构建决策树成为模式识别领域的一项研究热点。
使用增量训练的方式迭代训练决策树
融合Bagging与Boosting技术训练多棵决策树
对于波动不大、方差较小的数据集, 可以探寻一种比较稳定的分裂准则作为解决办法
总结
到此这篇决策树算法的实现和决策树算法的优缺点的介绍就介绍到这了,希望大家以后多多支持W3Cschool!

 免费AI编程助手
免费AI编程助手



